基本も基本、超基本の数学から始めるこのコーナーの目的は、「スタートの確認」と「ゴールの確認」にあります。公務員試験の数的推理は、微積分のような高度な知識は必要ありません。基礎的なテクニックを着実に積み上げることだけで正解に到達できます。第10回目は、場合の数のテクニックを「再」入門！

第1回　第2回　第3回　第4回 第5回　第6回　第7回　第8回　第9回　第10回 おまけ♪「数的推理を学ぶ前に」の見本画像

第10回　宝くじの当せん本数は？・・・場合の数

【問題】3桁の整数で、各桁の3つの数の和が9になるような数は全部でいくつあるか。

→　はじめは樹形図！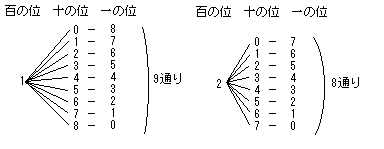

ここまで書いたら以降は推測がつくはず。 最後は、百の位が9で900の1通りとなるはず。（百の位が8なら、801、810の2通り） よって、9＋8＋7＋6＋5＋4＋3＋2＋1＝45（通り）

【問題でシミュレーション】

1〜50までの整数から、2つの異なる整数を取り出したとき、その2数の積が4の倍数になるものは何通りあるか。

	実戦的な考え方の手順は次のようになる （1） 4の倍数×□ （←　これは必ず4の倍数になるはず） （2） 偶数×偶数 （←　2×6も含まれるが、2×8は・と重なる） （3） 両者の重なりをひく （←　4の倍数×偶数をひく・・・？） ここまできて、（1）で4の倍数×奇数のみの数を考えればよいことに気づく！ 1〜50の中で4の倍数は50÷4＝12…2から12個。奇数は25個。 よって、4の倍数×奇数となる組は、　12×25＝300 偶数も25個あり、25個の中から2個を選ぶ「組合せ」は 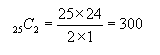300＋300＝600

600通り

第1回　第2回　第3回　第4回 第5回　第6回　第7回　第8回　第9回　第10回

Copyright (C)2009 SEMINET, KNoT All rights reserved.