ゼミネット公務員チャンネル・公務員試験対策講座／ここから確認・数的推理「再」入門

基本も基本、超基本の数学から始めるこのコーナーの目的は、「スタートの確認」と「ゴールの確認」にあります。公務員試験の数的推理は、微積分のような高度な知識は必要ありません。基礎的なテクニックを着実に積み上げることだけで正解に到達できます。第1回目は、最大公約数・最小公倍数のテクニックを「再」入門！

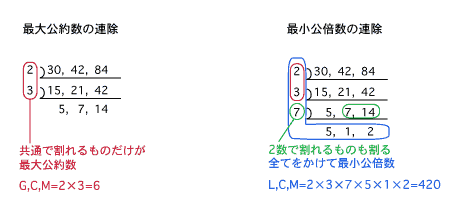
第1回　さかさま割り算覚えてる？・・・最大公約数・最小公倍数

【本試験レベルでシミュレーション】
2ケタの整数のうちで、6で割ると4余り、8で割ると6余る数は全部でいくつあるか。
1．3個	2．4個	3．5個	4．6個	5．7個


	ある数をＮとする。まず「6で割ると4余る」ということは、Ｎ＋2は6で割り切れる（＝6の倍数）。同じように「8で割ると6余る」ということは、Ｎ＋2は8でも割り切れる（＝8の倍数）。


	あまりの数にいくつ足せば割り切れるかをチェックする！ここで最大公約数　→Ｎ＋2は6と8の公倍数。　→6と8の最小公倍数の倍数。 2×2×2×3＝24　99÷24＝4…3 Ｎ＋2は（24、48、72、96）だからＮは（22、46、70、94）の4つとなる。

ゼミネット公務員講座では、図表・イラストを利用してわかりやすく解説しています。

次回は
「1から10を全部たすと？・・・数と規則」です。ご期待ください