ゼミネット公務員チャンネル・公務員試験対策講座／ここから確認・数的推理「再」入門

基本も基本、超基本の数学から始めるこのコーナーの目的は、「スタートの確認」と「ゴールの確認」にあります。公務員試験の数的推理は、微積分のような高度な知識は必要ありません。基礎的なテクニックを着実に積み上げることだけで正解に到達できます。第3回目は、Ｎ進法のテクニックを「再」入門！

第1回　第2回　第3回　第4回
第5回　第6回　第7回　第8回　第9回　第10回

第3回　あざらしは２進法？…Ｎ進法

10進法の「345」は、1の位が5、10の位が4、10²の位が3
6進法の「345」は、1の位が5、6の位が4、6²の位が3
だから、6進法の「345」を10進法にすると、1×5＋6×4＋6²×3＝137

10進法の「１９７」を6進法にするときは、さかさま割り算で6の束に分ける。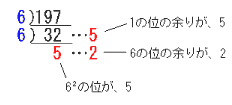

さかさまわり算図

197＝1×5＋6×2＋6²×5　だから、10進法の「197」は6進法で「525」

【問題でシミュレーション】
6進法であらわすと154となる数を、n進法であらわすと106になる。nはいくつか。


	6進法の「154」を10進法にすると、 4＋6×5＋6²×1＝70 n進法では「106」だから、6＋n×0＋n²×1＝70　この方程式を解いて、 n²＝64　よって、nは8進法となる。

ゼミネット公務員講座では、図表・イラストを利用してわかりやすく解説しています。

次回は
「移項・代入・同類項・・・方程式」です。ご期待ください。