基本も基本、超基本の数学から始めるこのコーナーの目的は、「スタートの確認」と「ゴールの確認」にあります。公務員試験の数的推理は、微積分のような高度な知識は必要ありません。基礎的なテクニックを着実に積み上げることだけで正解に到達できます。第7回目は、過不足算（不等式）のテクニックを「再」入門！

第1回　第2回　第3回　第4回 第5回　第6回　第7回　第8回　第9回　第10回

第7回　2個ずつだと余り、3個ずつじゃ足りない？・・・過不足算（不等式）

【問題】　あるグループで、ミカンを一人に2個ずつ分けると1個余り、3個ずつだと最後の一人に配るのに足りなくなる。グループの人数は何人から何人と考えられるか。 「2個ずつ分けると1個余り、3個ずつだと最後の一人に配るのに足りなくなる」という関係を図に画くと、

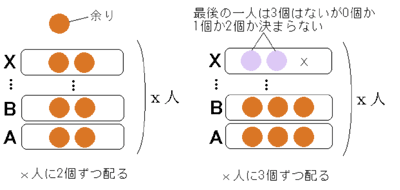この関係から (1)「ｘ人に2個ずつ配ると1個余る」ことから　→　ミカンの個数は 2ｘ＋1 (2)「ｘ人に3個ずつ配ると最後の一人の分が不足する」から →　ミカンの個数は3(ｘ−1)に最後の一人分を加え、 最も少なくて3(ｘ−1)、最も多くて3(ｘ−1)＋2 これを不等式であらわすと、　3(ｘ−1)≦2ｘ＋1≦3(ｘ−1)＋2 連立不等式を解いて、2≦ｘ≦4 よって、グループの人数は、2人から4人となる。

【問題でシミュレーション】

クラスの生徒が長いすに5人ずつ座ると3人座ることができず、7人ずつ座ると使わない長いすが1脚できる。生徒の数は何人と考えられるか。ただし、生徒の数は3の倍数とする。

	長いすの数をｘ脚とすると、「5人ずつ座ると3人余る」ことから、 生徒の数は　5ｘ＋3 (人) 7人ずつ座ると1脚使わないが、最後の長いすは7人全員座っているとは限らない。 最後の長いすに7人座っている場合　→　最大で7(ｘ−1) 最後の長いすには1人だけ座っている場合　→　最小で7(ｘ−2)＋1 このことから不等式をたてると、 　7(ｘ−2)＋1≦5ｘ＋3≦7(ｘ−1) これを解いて、　5≦ｘ≦8　 そして、長いすの数は整数であることから、生徒の人数は、 5×5＋3＝28（人）、5×6＋3＝33（人）、5×7＋3＝38（人）、5×8＋3＝43（人） 生徒の数は3の倍数であるから、33人。

33人

ゼミネット公務員講座では、図表・イラストを利用してわかりやすく解説しています。

次回は 「割り算・分数・割合だいじょうぶ？・・・比の問題」です。ご期待ください。

Copyright (C)2009 SEMINET, KNoT All rights reserved.